动态规划的各种类型
子序列DP
最长公共子序列
http://m.blog.csdn.net/article/details?id=6918848
树形DP
区间DP
状压DP
概率DP
数位DP
在信息学竞赛中,有一类与数位有关的区间统计问题。这类问题往往具有比较浓厚的数学味道,无法暴力求解,需要在数位上进行递推等操作。
在信息学竞赛中,有这样一类问题:求给定区间中,满足给定条件的某个 $D$ 进制数或此类数的数量。所求的限定条件往往与数位有关,例如数位之和、指定数码个数、数的大小顺序分组等等。题目给定的区间往往很大,无法采用朴素的方法求解。此时,我们就需要利用数位的性质,设计 $log(n)$ 级别复杂度的算法。
解决这类问题最基本的思想就是逐位确定的方法。
HDOJ 4722 Good Numbers
题意
如果一个数字的每个数位和能被10整除,那么它是good number,问 $[A,B]$ 区间里good number的数量。
数据
$0 \leq A,B \leq 10^{18}$
题解
$dp[pos][mod]$表示前 $pos$ 位,数位和取模10为 $mod$ ,后面数字任意且满足总数位和取模10为0的数量。记忆化深搜,基础入门题。
code
HDOJ 5642 King’s Order
题意
问长度为 $n$ 的字符串,由26个小写字母组成,满足相同的字母相邻出现不超过3个,问满足条件的方案数(mod 1000000007)。
数据
$0 \leq n \leq 2×10^{3}$
题解
$dp[pos][pre][mod]$表示前 $pos$ 位,当前位的字母是 $pre$,相同出现的个数为 $cnt$ 的方案数。
code
URAL 1057 Amount of Degrees
题意
求给定区间 $[X,Y]$ 中满足下列条件的整数个数:这个数恰好等于 $K$ 个互不相等的 $B$ 的整数次幂之和。
数据
$1 ≤ X ≤ Y ≤ 2^{31}−1$,$1 ≤ K ≤ 20$, $2 ≤ B ≤ 10$
题解
所求的数为互不相等的幂之和,亦即其 $B$ 进制表示的各位数字都只能是 $0$ 和 $1$。因此,我们只需讨论二进制的情况,其他进制都可以转化为二进制求解。
那么问题和上题几乎一样,$dp[pos][mod]$表示前 $pos$ 位,相同出现 $1$ 的个数为 $cnt$ 的方案数。
code
SPOJ SQRTBIT Sorted bit squence
题意
将区间 $[m,n]$ 内的所有整数按照其二进制表示中 $1$ 的数量从小到大排序。如果 $1$ 的数量相同,则按照数的大小排序。求这个序列中的第 $k$ 个数。
数据
$m × n ≥ 0$, $-2^{31} ≤ m ≤ n ≤ 2^{31}-1$,$1 ≤ k ≤ min(n − m + 1, 2147473547)$
题解
我们首先考虑 $m,n>0$ 的情况。
由于排序的第一关键字是 $1$ 的数量,第二关键字是数的大小,因此我们很容易确定答案中 $1$ 的个数:依次统计区间 $[m,n]$ 内二进制表示中含 $1$ 的数量为$0,1,2,…$的数,直到累加的答案超过 $k$ ,则当前值就是答案含 $1$ 的个数,假设是 $s$ 。利用上题的方法处理。同时,我们也求出了答案是第几个 $[m,n]$ 中含 $s$ 个 $1$ 的数。因此,只需二分答案,求出$[m,ans]$ 中含 $s$ 个 $1$ 的数的个数进行判断即可。
$m<0$的情况也不难处理,直接将负数视为32位无符号数(或者直接使用 long long 数据类型),采用同正数一样的处理方法(需特殊处理$n=0$ 的情况)。
code
SPOJ BIGSEQ Sequence
题意
给定所有 $K$ 位二进制数:$0,1,…,2^{K}-1$。你需要将它们分成恰好 $M$ 组,每组都是原序列中连续的一些数。设 $S_i$($1 ≤ i ≤ M$)表示第 $i$ 组中所有数的二进制表示中 $1$ 的个数,$S$ 等于所有$S_i$中的最大值。你的任务是令 $S$ 最小。
数据
$1 ≤ K ≤ 100$, $1 ≤ M ≤ 100$, $M ≤ 2^K$
题解
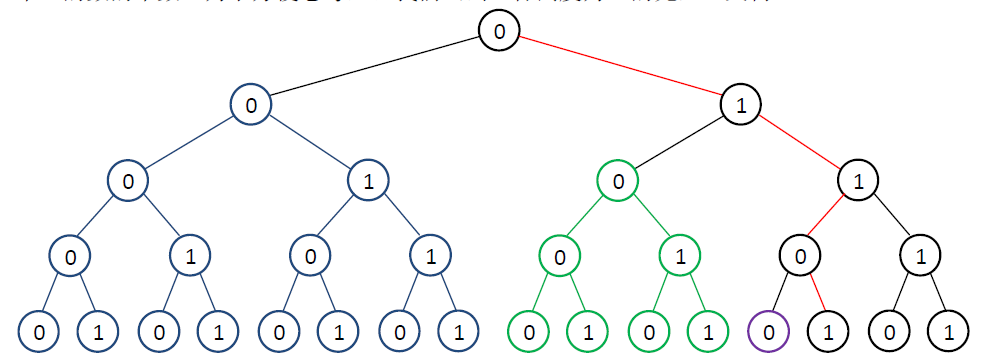
代码解释:$d[i]=2^i$,$f[i]$ 表示高度为i的左子树中所有数的二进制表示中 $1$ 的个数(叶子结点高度为0)。
code